Voici les questions auxquelles je veux pouvoir répondre :
- je veux faire une pâte d'un poids donné, quels poids d'eau, de farine et de levain dois-je utiliser ?
- je dispose d'un certain poids de levain, quels poids d'eau et de farine dois-je lui ajouter ?
- j'ai une recette de pain à la levure, comment le convertir en recette de pain au levain ?
Afin d'écrire des programmes qui permettent d'automatiser les calculs, il me faut déterminer les formules à appliquer.
Les formules
Le taux d'hydratation
Voici un préambule nécessaire sur le taux d'hydratation en boulangerie :
- pf : poids de la farine ;
- pe : poids de l'eau ;
- pp : poids de la pâte, c'est à dire la farine et l'eau mélangées ;
- th : taux d'hydratation.
La définition du taux d'hydratation :
th = pe / pf pe = pf * th pf = pe / th
Et voici d'autres relations avec le poids de la pâte qui seront bien utiles pour la suite.
D'abord, le poids total de la pâte en fonction des poids de la farine et de l'eau :
pp = pf + pe
= pf + pf * th
= (1 + th) * pf
pp = pe + pf
= pe + pe / th
= (1 + 1 / th) * pe
Et enfin les poids de la farine et de l'eau en fonction du poids total de la pâte :
pf = pp / (1 + th) pe = pf * th = pp * th / (1 + th)
Applications
Les données sont les suivantes :
- ptp : poids total de la pâte (eau + farine + levain) ;
- thl : taux d'hydratation du levain ;
- thp : taux d'hydratation de la pâte ;
- tlf : taux de la farine du levain par rapport à la farine ;
- pf : le poids de la farine ;
- pe : le poids de l'eau ;
- pfl : le poids de farine dans le levain ;
- pel : le poids de l'eau dans le levain ;
- pl : poids du levain (eau + farine) ;
- pte : le poids total d'eau (l'eau ajoutée pe + celle contenue dans le levain pel) ;
- ptf : le poids total de farine (y compris celle contenue dans le levain pf + pfl).
Supposons que l'on connaisse le poids de la farine pfl contenue dans le levain. On pourrait effectuer une chaîne de calculs rien qu'en posant les définitions. La valeur obtenue sur une ligne est reportée dans la suivante et ainsi de suite :
pf = pfl / tlf ptf = pf + pfl pte = ptf * thp pel = pfl * thl pe = pte - pel
Parcourons cette chaîne sans faire des calculs numériques mais en substituant les définitions dans les lignes qui suivent.
Eliminons pf :
ptf = pfl / tlf + pfl
= (1 / tlf + 1) * pfl
pte = ptf * thp
pel = pfl * thl
pe = pte - pel
Eliminons ptf :
pte = (1 / tlf + 1) * pfl * thp pel = pfl * thl pe = pte - pel
Eliminons pte et pel :
pe = (1 / tlf + 1) * pfl * thp - pfl * thl = [(1 / tlf + 1) * thp - thl] * pfl
Récapitulons, pfl étant supposé donné au départ :
pfl pf = pfl / tlf ptf = (1 / tlf + 1) * pfl pte = (1 / tlf + 1) * pfl * thp pel = pfl * thl pe = [(1 / tlf + 1) * thp - thl] * pfl
pfl n'est en fait pas une donnée de départ, il faut donc le calculer.
Poids de la pâte imposé
Si ptp est imposé, c'est pas très compliqué (cf préambule sur le taux d'hydratation pour la première ligne) :
ptf = ptp / (1 + thp)
(1 / tlf + 1) * pfl = ptp / (1 + thp)
pfl = ptp / (1 + thp) / (1 / tlf + 1)
= ptp * tlf / (1 + thp) / (1 + tlf)
et :
pl = (1 + thl) * pfl
Les données d'entrée sont donc :
- ptp : poids total de la pâte (eau + farine + levain) ;
- thl : taux d'hydratation du levain ;
- thp : taux d'hydratation de la pâte ;
- tlf : taux de la farine du levain par rapport à la farine ;
et les données de sortie sont :
- pf : le poids de la farine ;
- pe : le poids de l'eau ;
- pl : poids du levain ;
Application numérique
Données d'entrée
ptp = 1000 thp = 0.6 thl = 0.8 tlf = 0.3
Voici le déroulé des formules :
pfl = 1000 * 0.3 / (1 + 0.6) / (1 + 0.3) = 144.23 pf = 144.23 / 0.3 = 480.77 ptf = (1 / 0.3 + 1) * 144.23 = 625 pte = (1 / 0.3 + 1) * 144.23 * 0.6 = 375 pel = 144.23 * 0.8 = 115.38 pe = [(1 / 0.3 + 1) * 0.6 - 0.8] * 144.23 = 259.61 pl = (1 + 0.8) * 144.23 = 259.61
Utilisation d'un tableur
Certains préféreront utiliser un tableur. Son avantage est d'être plus visuel et de faire apparaître les calculs intermédiaires. Le fichier au format ods (LibreOffice et OpenOffice) pate-imposee.ods est téléchargeable.
En affichant les formules :
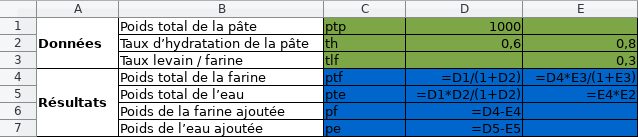
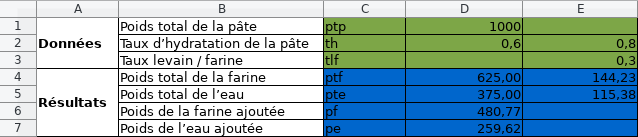
Et en affichant les valeurs :
Production d'une pâte par plusieurs rafraîchis
Nouvelle utilisation du tableur pour effectuer la même opération plusieurs fois de suite. Le levain est rafraîchi plusieurs fois jusqu'à obtenir la quantité de pâte désirée. Le fichier au format ods (LibreOffice et OpenOffice) pate-imposee-iteratif.ods est téléchargeable.
En affichant les formules :

Et en affichant les valeurs :

Interprétation du tableau :
- premier rafraîchi : on prend 13,8 de levain hydraté à 80% auquel on ajoute 25,6 de farine et 20,5 d'eau, ce qui donne 59,9 de pâte hydratée à 80% et dont 30% de la farine provient du levain ;
- deuxième rafraîchi : on prend 59,9 de levain hydraté à 80% auquel on ajoute 110,9 de farine et 88,8 d'eau, ce qui donne 259,6 de pâte hydratée à 80% et dont 30% de la farine provient du levain ;
- troisième rafraîchi : on prend 259,6 de levain hydraté à 80% auquel on ajoute 480,8 de farine et 259,6 d'eau, ce qui donne 1000 de pâte hydratée à 60% et dont 30% de la farine provient du levain.
Le sel n'entre dans la composition de la pâte que lors du dernier "rafraîchi".
Poids du levain imposé
Si le poids du levain pl est imposé, c'est beaucoup plus facile (idem préambule) pour trouver le poids de la farine du levain à partir de pl :
pfl = pl / (1 + thl)
Les données d'entrée sont donc :
- pl : poids du levain ;
- thl : taux d'hydratation du levain ;
- thp : taux d'hydratation de la pâte ;
- tlf : taux de la farine du levain par rapport à la farine ;
et les données de sortie :
- pf : poids de la farine ;
- pe : poids de l'eau ;
- ptp : poids total de la pâte (eau + farine + levain) ;
Application numérique :
pl = 150 thl = 0.8 thp = 0.6 tlf = 0.3
Voici le déroulé des formules :
pfl = 150 / (1 + 0.8) = 83.33 pf = 83.33 / 0.3 = 277.77 ptf = (1 / 0.3 + 1) * 83.33 = 361.11 pte = (1 / 0.3 + 1) * 83.33 * 0.6 = 216.67 pel = 83.33 * 0.8 = 66.67 pe = [(1 / 0.3 + 1) * 0.6 - 0.8] * 83.33 = 150 ptp = 361.11 + 216.67 = 577.78
Utilisation d'un tableur
Le fichier au format ods levain-impose.ods est téléchargeable.
En affichant les formules :
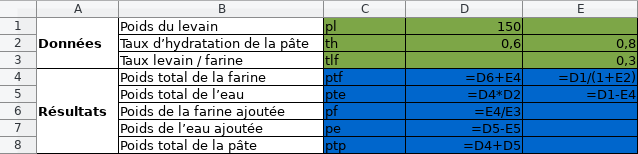
Et en affichant les valeurs :
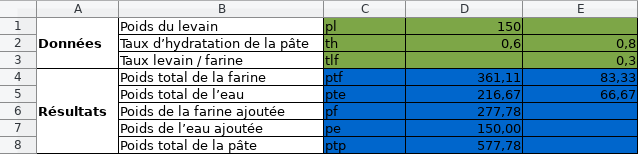
Pâte équivalente
Les données d'entrée sont :
- pte : le poids de l'eau ;
- ptf : le poids de la farine ;
- thl : taux d'hydratation du levain ;
- tlf : taux de la farine du levain par rapport à la farine ;
et on veut obtenir :
- pf : poids de la farine ;
- pe : poids de l'eau ;
- pl : poids du levain (eau + farine).
Posons les définitions :
pe = pte - pel pf = ptf - pfl pel = pfl / thl pl = pfl + pel pl = pf * tlf
Eliminons pel :
pe = pte - pfl / thl pf = ptf - pfl pl = pfl + pfl / thl = (1 + 1 / thl) * pfl pl = pf * tlf
Eliminons pfl :
pe = pte - pl / [(1 + 1 / thl) * thl] pf = ptf - pl / (1 + 1 / thl) pl = pf * tlf
Eliminons pl :
pe = pte - pf * tlf / [(1 + 1 / thl) * thl] pf = ptf - pf * tlf / (1 + 1 / thl) pe = pte - ptf * tlf / [1 + (1 + tlf) * thl] pf = ptf / [1 + tlf / (1 + 1 / thl)]
Application numérique :
ptf = 500 pte = 300 thl = 0.7 tlf = 0.4
Voici le déroulé des formules :
pe = 300 - 500 * 0.4 / [1 + (1 + 0.4) * 0.7] = 198.99 pf = 500 / (1 + 0.4 / (1 + 1 / 0.7)) = 429.29 pl = 429.29 * 0.4 = 171.72
Vérifications :
pfl = 500 - 429.29 = 70.71 pel = 300 - 198.99 = 101.01 pl = 70.71 + 101.01 = 171.72 -> OK thl = 70.71 / 101.01 = 0.7 -> OK
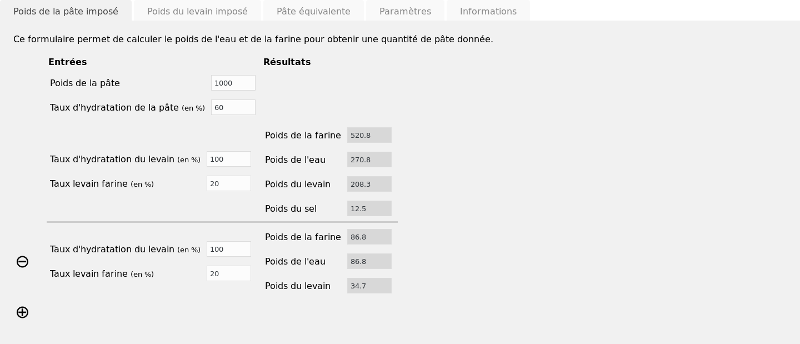
Les formulaires en ligne
Je mets à votre disposition des formulaires de calculs de boulangerie qui automatisent les calculs présentés ci-dessus.
Vous pouvez retrouver le projet complet sous Github.